Answer:
0.013 = 1.3% probability that at least one is taller than 21 inches
Explanation:
To solve this question, we need to understand the binomial distribution and the normal distribution.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Proportion of male dogs taller than 21 inches:
A mean of 19.5 inches and a standard deviation of 0.5 inches. This means that
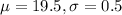
This proportion is 1 subtracted by the pvalue of Z when X = 21.

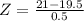
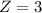
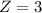 has a pvalue of 0.9987
has a pvalue of 0.9987
1 - 0.9987 = 0.0013.
In a random sample of 10 male Shar Pei dogs what is the probability that at least one is taller than 21 inches?
0.0013 of the dogs are taller than 21 inches, so
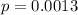
10 dogs, so

Either no dog is taller than 21 inches, or at least one is. The sum of the probabilities of these events is 1. So
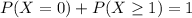
We want
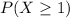
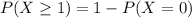
In which

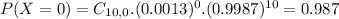
Then
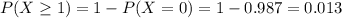
0.013 = 1.3% probability that at least one is taller than 21 inches