Question

Explain the special pattern for sketching a parabola

Answer 1

the parabola can be written as:

f(x) = y = a*x^2 + b*x + c

first step.

find the vertex at:

x = -b/2a

the vertex will be the point (-b/2a, f(-b/2a))

now, if a is positive, then the arms of the parabola go up, if a is negative, the arms of the parabola go down.

The next step is to see if we have real roots by using the Bhaskara's equation:

`x = (-b +-√(b^2 -4ac) )/(2a)`

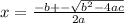
Now, draw the vertex, after that draw the values of the roots in the x-axis, and now conect the points with the general draw of the parabola.

If you do not have any real roots, you can feed into the parabola some different values of x around the vertex

for example at:

x = (-b/2a) + 1 and x = (-b/2a) - 1

those two values should give the same value of y, and now you can connect the vertex with those two points.

If you want a more exact drawing, you can add more points (like x = (-b/2a) + 3 and x = (-b/2a) - 3) and connect them, as more points you add, the best sketch you will have.