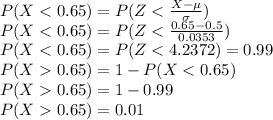Question

You plan to conduct a marketing experiment in which students are to taste one of two different brands of soft drink. Their task is to correctly identify the brand tasted. You select a random sample of 200 students and assume that the students have no ability to distinguish between the two brands. (Hint: if an individual has no ability to distinguish between the two soft drinks, then each brand is equally likely to be selected.)(a) What is the probability that the sample will have between 50% and 60% of the identification correct?(b) The probability is 90% that the sample percentage contained within what symmetrical limits of the population percentage?(c) What is the probability that the sample percentage of correct identifications is greater than 65%?

Answer 1

a) probability that the sample will have between 50% and 60% of the identification correct = 0.498

b) The probability is 90% that the sample percentage is contained 45.5% and 54.5% of the population percentage

c) Probability that the sample percentage of correct identifications is greater than 65% = 0.01

Explanation:

Sample size, n = 200

Since the brands are equally likely, p = 0.5, q = 0.5

The Standard deviation,
`\sigma_p = \sqrt{(pq)/(n) }`

`\sigma_p = \sqrt{(0.5 * 0.5)/(200) } \\\sigma_p = 0.0353`

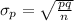
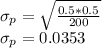
a) probability that the sample will have between 50% and 60% of the identification correct.

`P(0.5 < X < 0.6) = P((0.5 - 0.5)/(0.0353) < Z < (0.6 - 0.5)/(0.0353) )\\P(0.5 < X < 0.6) = P( 0 < Z < 2.832)\\P(0.5 < X < 0.6) = P(Z < 2.832) - P(Z < 0)\\P(0.5 < X < 0.6) = 0.998 - 0.5\\P(0.5 < X < 0.6) = 0.498`

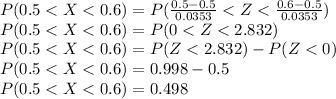
Probability that the sample will have between 50% and 60% of the identification correct is 0.498

b) p = 90% = 0.9

Getting the z value using excel:

z = (=NORMSINV(0.9) )

z = 1.281552 = 1.28 ( 2 dp)

Then we can calculate the symmetric limits of the population percentage as follows:

`z = (X - \mu)/(\sigma_p)`

`-1.28 = (X_1 - 0.5)/(0.0353) \\-1.28 * 0.0353 = X_1 - 0.5\\-0.045+ 0.5 = X_1\\X_1 = 0.455`

`1.28 = (X_2 - 0.5)/(0.0353) \\1.28 * 0.0353 = X_2 - 0.5\\0.045+ 0.5 = X_2\\X_2 = 0.545`

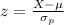
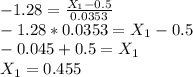
The probability is 90% that the sample percentage is contained 45.5% and 54.5% of the population percentage

c) Probability that the sample percentage of correct identifications is greater than 65%

P(X>0.65) = 1 - P(X<0.65)

`P(X<0.65) = P(Z< (X - \mu)/(\sigma) )\\P(X<0.65) = P(Z< (0.65 - 0.5)/(0.0353) )\\P(X<0.65) = P(Z < 4.2372) = 0.99\\P(X>0.65) = 1 - P(X<0.65)\\P(X>0.65) = 1 - 0.99\\P(X>0.65) = 0.01`