Question

Please answer correctly !!!!!!! Will mark Brianliest !!!!!!!!!!!

Answer 1

`x=-2\\x=2`

(You only need to give one solution)

Explanation:

We have the following equation

`(x^2+1)^2-5x^2-5=0`

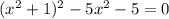
First, we need to foil out the parenthesis

`x^4+2x^2+1-5x^2-5=0`

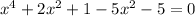
Now we can combine the like terms

`x^4-3x^2-4=0`

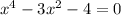
Now, we need to factor this equation.

To factor this, we need to find a set of numbers that add together to get -3 and multiply to give us -4.

The pair of numbers that would do this would be 1 and -4.

This means that our factored form would be

`(x^2-4)(x^2+1)=0`

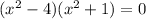
As the first binomial is a difference of squares, it can be factored futher into

`(x^2+1)(x+2)(x-2)=0`

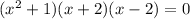
Now, we can get our solutions.

The first binomial will produce two complex (Not real) solutions.

`x+2=0\\\\x=-2`

`x-2=0\\\\x=2`

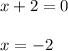
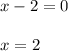
So our solutions to this equation are

`x=-2\\x=2`