Answer:
a)
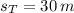 , b)
, b)
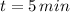 , c)
, c)
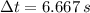 , d)
, d)
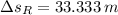 , e)
, e)
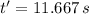 , f) The rabbit won the race.
, f) The rabbit won the race.
Step-by-step explanation:
a) As turtle moves at constant speed, its position is determined by the following formula:
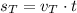
Where:
 - Time, measured in seconds.
- Time, measured in seconds.
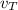 - Velocity of the turtle, measured in meters per second.
- Velocity of the turtle, measured in meters per second.
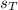 - Position of the turtle, measured in meters.
- Position of the turtle, measured in meters.
Then, the position of the turtle when the rabbit starts to run is:
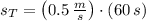
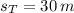
The position of the turtle when the rabbit starts to run is 30 meters.
b) The time needed for the turtle to finish the race is:
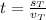
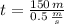
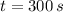
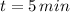
The time needed for the turtle to finish the race is 5 minutes.
c) As rabbit experiments a constant acceleration until maximum velocity is reached and moves at constant speed afterwards, the time required to reach such speed is:
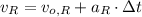
Where:
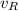 - Final velocity of the rabbit, measured in meters per second.
- Final velocity of the rabbit, measured in meters per second.
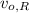 - Initial velocity of the rabbit, measured in meters per second.
- Initial velocity of the rabbit, measured in meters per second.
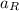 - Acceleration of the rabbit, measured in
- Acceleration of the rabbit, measured in
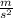 .
.
 - Running time, measured in second.
- Running time, measured in second.
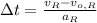
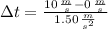
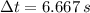
The time taken by the rabbit to reach maximum speed is 6.667 s.
d) On the other hand, the position reached by the rabbit when maximum speed is reached is determined by the following equation of motion:
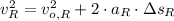
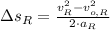
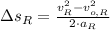
Where
 is the travelled distance of the rabbit from rest to maximum speed.
is the travelled distance of the rabbit from rest to maximum speed.
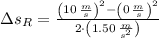
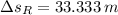
The distance travelled by the rabbit from rest to maximum speed is 33.333 meters.
e) The time required for the rabbit to finish the race can be determined by the following expression:

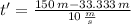
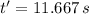
The time required for the rabbit from rest to maximum speed is 11.667 seconds.
f) The animal with the lowest time wins the race. Now, each running time is determined:
Turtle:
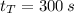
Rabbit:
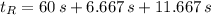
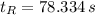
The rabbit won the race as
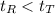 .
.