Question

The drawing shows three identical springs hanging from the ceiling. Nothing is attached to the first spring, whereas a 4.50-N block hangs from the second spring. A block of unknown weight hangs from the third spring. From the drawing, determine (a) the spring constant (in N/m) and (b) the weight of the block hanging from the third spring

Answer 1

a. 30 N / m

b. 9.0 N

Step-by-step explanation:

Given that

Unstretched length of the spring,
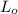`L_o` = 20.0cm = 0.2m

a) When the mass of 4.5N is hanging from the second spring, then extended length Is

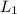`L_1` = 35.0cm = 0.35m

So, the change in spring length when mass hangs is

`x = L_1 - L_o`

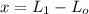
= (0.35 - 0.20) m

= 0.15m

As spring are identical

Let us assume that the spring constant be "k", so at equilibrium

Restoring Force on spring = Block weightage

kx = W = 4.50

`k= (4.50)/(x) = (4.50)/(0.15)`

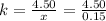
= 30 N / m

b) Now for the third spring, stretched the length of spring is

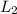`L_2` = 50cm = 0.5m

So, the change in spring length is

`x'= L_2 - L_o`

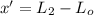
= (0.5-0.20)m

= 0.30m

At equilibrium,

Restoring Force on spring = Block weightage

Now using all mentioned and computed values in above,

`W'= kx'`

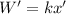
= 30(0.3)

= 9.0 N