Answer:
11.11% probability that it will rain on the day of Marie's wedding, given the weatherman forecasts rain
Explanation:
Bayes Theorem:
Two events, A and B.
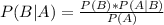
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.
In this question:
Event A: Forecast of rain.
Event B: Raining.
In recent years, it has rained only 5 days each year.
A year has 365 days. So
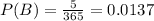
When it actually rains, the weatherman correctly forecasts rain 90% of the time.
This means that

Probability of forecast of rain:
90% of 0.0137(forecast and rains)
10% of 1 - 0.0137 = 0.9863(forecast, but does not rain)
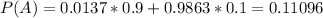
What is the probability that it will rain on the day of Marie's wedding, given the weatherman forecasts rain
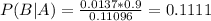
11.11% probability that it will rain on the day of Marie's wedding, given the weatherman forecasts rain