Question

Regular ATM Non regular ATM

n = 200 n = 200
x-bar = 143 x-bar = 133
The managers of a regional bank in Florida believe that customers who regularly use their ATM cards (regular is defined as at least one time per week) are more profitable to the bank overall than customers who do not regularly use their ATM cards. A sample of 200 of the bank’s customers in each category was selected. An accounting was performed to determine the profit generated from each customer. The following sample data were observed. Regular ATM Non regular ATM n = 200 n = 200 x-bar = 143 x-bar = 133 Assume the following population standard deviations: 30 and 34, for regular ATM and non-regular ATM, respectively.
Using a level of significance of 0.05, what conclusion should the bank’s manager reach based on the sample data? Show all the five steps of the hypothesis testing.

Answer 1

Conclusion

We can conclude that the believe of the mangers of the regional banks is true

Explanation:

From the question we are told that

The sample size is n = 200

The mean for Regular user is
`\= x_1 = 143`

The mean for Non regular is
`\r x_2 = 133`

The standard deviation for Regular is
`\sigma_1 = 30`

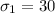
The standard deviation for Non regular is
`\sigma _2 = 34`

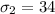
The level of significance is
`\alpha = 0.0 5`

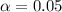
The null hypothesis is

`H_0 : \r x_1 = \r x_2`

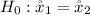
The alternative hypothesis is

`Ha: \r x_1 > \r x_2`

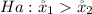
The test statistics is mathematically represented as

`Z = \frac{\r x _1 - \r x_2}{\sqrt{(\sima_1^)/(n) } + (\sigma_2^2)/(n) }`

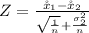
substituting values

`Z = \frac{143 - 133}{\sqrt{(30^2)/(200) } + (34^2)/(200) }`

`Z = 3.12`

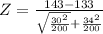
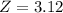
Now the critical value of the level of significance obtained from the z-table is

`t_(\alpha ) = 1.645`

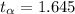
So given the fact as seen from the above calculation that
`Z > t_(\alpha )`

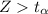
Then the Null hypothesis would be rejected as there is no sufficient evidence to back up the null hypothesis [Which stated that the profit from both users are the same ]