Question

Existing research states that the proportion of households in a city owning a computer is 30%. However, a local politician believes that that number is wrong. He randomly selects 200 families and finds that 68 of them have computers. Please conduct a formal hypothesis test to verify if the politician’s claim is credible.

Select one:
a. H0: p = 0.3, HA: p ≠ 0.3, z = 1.23, p-value = 0.2187, so we conclude there is insufficient evidence for the politician’s claim and fail to reject the null hypothesis.
b. H0: p = 0.3, HA: p > 0.3, z = 1.23, p-value = 0.1093, so we conclude there is insufficient evidence for the politician’s claim and reject the null hypothesis.
c. H0: p = 0.3, HA: p < 0.3, z = 1.23, p-value = 0.8907, so we conclude that there is evidence for the politician’s claim and reject the null hypothesis.
d. H0: p = 0.3, HA: p ≠ 0.3, z = 1.23, p-value = 0.2187, so we conclude that there is evidence for the politician’s claim and reject the null hypothesis.

Answer 1

`z=\frac{0.34 -0.3}{\sqrt{(0.3(1-0.3))/(200)}}=1.23`

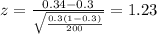
Now we can calculate the p value as:

`p_v =2*P(z>1.23)=0.2187`

And the best conclusion would be:

a. H0: p = 0.3, HA: p ≠ 0.3, z = 1.23, p-value = 0.2187, so we conclude there is insufficient evidence for the politician’s claim and fail to reject the null hypothesis.

Explanation:

Information given

n=200 represent the random sample taken

X=68 represent the number of families with computers

estimated proportion of families with computers

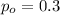`p_o=0.3` is the value to verify

z would represent the statistic

`p_v` represent the p value

Hypothesis to test

We want to check if the true proportion is equal to 0.3 or not.:

Null hypothesis:
`p=0.3`

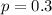
Alternative hypothesis:
`p \\eq 0.3`

The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing we got:

`z=\frac{0.34 -0.3}{\sqrt{(0.3(1-0.3))/(200)}}=1.23`

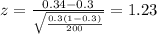
Now we can calculate the p value as:

`p_v =2*P(z>1.23)=0.2187`

And the best conclusion would be:

a. H0: p = 0.3, HA: p ≠ 0.3, z = 1.23, p-value = 0.2187, so we conclude there is insufficient evidence for the politician’s claim and fail to reject the null hypothesis.