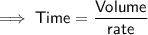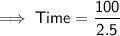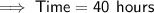Answer:
40 hours
Explanation:
The swimming pool can be modeled as a rectangular prism.
Volume of a rectangular prism
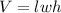
where:
- l = length
- w = width
- h = height
First, calculate the volume of water needed:
Given:
Substitute the given values into the formula and solve for V:
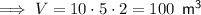
If the water flows as a rate of 2.5 m³/h, divide the volume by the rate to calculate how long it will take to fill the pool: