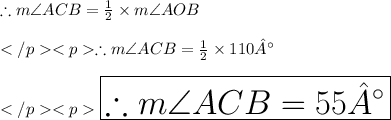Answer:
55°
Explanation:
In circle with center O, OA and OB are radii and PA and PB are tangents drawn from external point P.
Since, tangent is perpendicular to the radius of the circle.
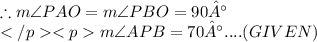
In quadrilateral PAOB,
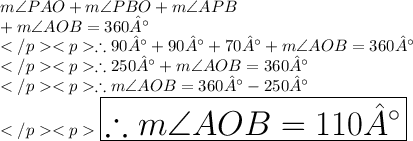
Since, angle subtended at the circumference of the circle is half of the angle subtended at the centre of the circle.