Question

Fill in the blanks for the following:

Arigid container of volume 100.0 Liters contains Oxygen gas. It is at room temperature (293 Kelvin), and is at atmospheric pressure (absolute pressure, meaning the gauge pressure is zero). Therefore, the number of moles of Oxygen molecules . Also, the rms-velocity inside is ________of these Oxygen molecules is most nearly ______, which is______ the rms-speed of the Nitrogen molecules just outside the container (the rigid container and its surroundings are in thermal equilibrium).

Answer 1

a. 4.21 moles

b. 478.6 m/s

c. 1.5 times the root mean square velocity of the nitrogen gas outside the tank

Step-by-step explanation:

Volume of container = 100.0 L

Temperature = 293 K

pressure = 1 atm = 1.01325 bar

number of moles n = ?

using the gas equation PV = nRT

n = PV/RT

R = 0.08206 L-atm-
`mol^(-1)`
`K^(-1)`

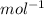
Therefore,

n = (1.01325 x 100)/(0.08206 x 293)

n = 101.325/24.04 = 4.21 moles

The equation for root mean square velocity is

Vrms =
`\sqrt{(3RT)/(M) }`

R = 8.314 J/mol-K

where M is the molar mass of oxygen gas = 31.9 g/mol = 0.0319 kg/mol

Vrms =
`\sqrt{(3*8.314*293)/(0.0319) }`= 478.6 m/s

For Nitrogen in thermal equilibrium with the oxygen, the root mean square velocity of the nitrogen will be proportional to the root mean square velocity of the oxygen by the relationship

`(Voxy)/(Vnit)` =
`\sqrt{(Mnit)/(Moxy) }`

where

Voxy = root mean square velocity of oxygen = 478.6 m/s

Vnit = root mean square velocity of nitrogen = ?

Moxy = Molar mass of oxygen = 31.9 g/mol

Mnit = Molar mass of nitrogen = 14.00 g/mol

`(478.6)/(Vnit)` =
`\sqrt{(14.0)/(31.9) }`

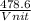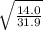
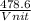`(478.6)/(Vnit)` = 0.66

Vnit = 0.66 x 478.6 = 315.876 m/s

the root mean square velocity of the oxygen gas is

478.6/315.876 = 1.5 times the root mean square velocity of the nitrogen gas outside the tank