Question

In the year 2004, a company made $5.2 million in profit. For each consecutive year after that, their profit increased by 15%. How much would the company's profit be in the year 2007, to the nearest tenth of a million dollars?

Answer 1

The company's profit in the year 2007 would be of $7.9 million.

Explanation:

The profit of the company, in t years after 2004, is given by the following equation:

`P(t) = P(0)(1+r)^(t)`

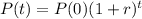
In which P(0) is the profit in 2004, and r is the growth rate, as a decimal.

In the year 2004, a company made $5.2 million in profit.

This means that
`P(0) = 5.2`

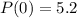
For each consecutive year after that, their profit increased by 15%.

This means that
`r = 0.15`

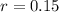
Then

`P(t) = P(0)(1+r)^(t)`

`P(t) = 5.2(1+0.15)^(t)`

`P(t) = 5.2(1.15)^(t)`

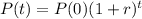
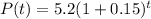
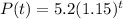
How much would the company's profit be in the year 2007, to the nearest tenth of a million dollars?

2007 is 2007 - 2004 = 3 years after 2004. So this is P(3).

`P(t) = 5.2(1.15)^(t)`

`P(3) = 5.2(1.15)^(3) = 7.9`

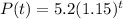
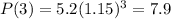
The company's profit in the year 2007 would be of $7.9 million.