Answer:
i ≈ 530 inches (to the nearest inch)
Explanation:
Check the diagram in the attachment. Using sin rule to get the length of i.
According to the rule
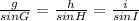
Given h = 300 inches, ∠G=30° and ∠H=29°; we can use the relationship below to get length of i;
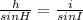 ... 1
... 1
Since sum of angle in a triangle is 180°, then ∠G+∠H+∠I = 180°
30°+29°+∠I = 180°
∠I = 180°-(30°+29°)
∠I = 180°-59°
∠I = 121°
Applying equation 1;
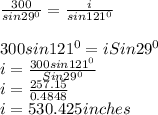
i ≈ 530 inches (to the nearest inch)