Answer:
Therefore, the mean and the standard deviation for the number of electrical outages (respectively) are 0.26 and 0.5765 respectively.
Explanation:
Given the probability distribution table below:
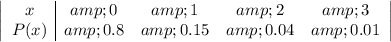
(a)Mean
Expected Value,
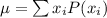
=(0*0.8)+(1*0.15)+(2*0.04)+(3*0.01)
=0+0.15+0.08+0.03
Mean=0.26
(b)Standard Deviation
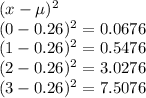
Standard Deviation
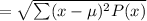
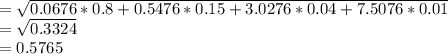
Therefore, the mean and the standard deviation for the number of electrical outages (respectively) are 0.26 and 0.5765 respectively.