Answer:
ΔF = 0.21 N
Step-by-step explanation:
For this exercise that does not ask for the change in weight we must use the law of universal gravitation
F = G M m / r²
where r is the distance from the center of the Earth, in the lower part of the building is
r =
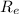
for the upper part of the building h = 1 mile = 1609.34 m
r =R_{e} + h
the weight or the force of attraction of gravity on the floor is F = 817 N, therefore the equation remains
817 = (G M m / R_{e}²)
let's find this force for the top of the building
F` = G M m / (R_{e} + h)²
let's take out R_{e} common factor
F ’= (G M m / R_{e}²) 1 / (1 + h / R_{e})²2
F ’= (G M m R_{e}²) (1 + h / R_{e})⁻²
as the quantity h /R_{e} = 1609 / 6.37 10⁶ << 1 we can make a series space
(1 + x)⁻² = 1 -2 x + ...
we substitute
F ’= (GMm /R_{e}²) (1 - 2 1609 / 6.37 10⁶)
F ’= (GMm /R_{e}²) (1 - 2.53 10⁻⁴) = (GMm / R_{e}²) 0.99974
F ’= 817 0.99974
F ’= 816.79 N
weight Change
ΔF = ΔW = 817 - 816.79
ΔF = 0.21 N
as we see this is a very small amount