Question

The marginal profit in dollars on Brie cheese sold at a cheese store is given by P'(x)=x(60x^2+30x), where x is the amunt of cheese sold, in hundreds of pounds. The "profit" is -$80 when no cheese is sold.a. Find the profit functionb. Find the profit from selling 200lbs of Brie Cheese

Answer 1

a)
`P(x) = 15x^(4) + 10x^(3) - 80`

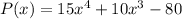
b) The profit from selling 200lbs of Brie Cheese is $240.

Explanation:

a. Find the profit function

We have that:

`P'(x) = 60x^(3) + 30x^(2)`

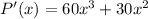
The profit function is P(x), which is the integral of P'(x).

So

`P(x) = \int {P'(x)} \, dx = \int {60x^(3) + 30x^(2)} \, dx = (60x^(4))/(4) + (30x^(3))/(3) + K = 15x^(4) + 10x^(3) + K`

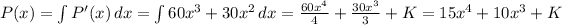
There, I applied the integral rules of sum and power.

Since P(0) = -80, K = -80

Then

`P(x) = 15x^(4) + 10x^(3) - 80`

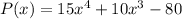
b. Find the profit from selling 200lbs of Brie Cheese

200 lbs is 200/100 = 2 hundreds of pounds.

So this is P(2).

`P(x) = 15x^(4) + 10x^(3) - 80`

`P(2) = 15*2^(4) + 10*2^(3) - 80`

`P(2) = 240`

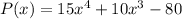
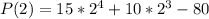
The profit from selling 200lbs of Brie Cheese is $240.