Question

A 0.23 kg rock is projected from the edge of the top of a building with an initial velocity of 11.5 m/s at an angle 46? above the horizontal. The building is 7.67 m in height.At what horizontal distance, x, from the base of the building will the rock strike the ground? Assume the ground is level and that the side of the building is vertical. The acceleration of gravity is 9.8 m/s2.

Answer 1

x = 17,978 m

Step-by-step explanation:

This is a projectile launching exercise, to solve it the time it takes to reach the ground in the vertical movement and the time it takes to make the horizontal tour, by which we begin by finding the time it takes to reach the ground in the vertical movement

y = y₀ +
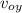`v_(oy)` t - ½ g t²

let's use trigonometry to find the components of the initial velocity

sin 46 = v_{oy} / v₀

cos 46 = v₀ₓ / v₀

v_{oy} = vo sin 46

v₀ₓ = vo cos 46

v_{oy} = 11.5 sin 46 = 8.27 m / s

v₀ₓ = 11.5 cos 45 = 7.99 m / s

the height of the building is y₀ = 7.67 m, we substitute

0 = 7.67 + 8.27 t - ½ 9.8 t²

t² - 1,688 t - 1,565 = 0

let's solve the quadratic equation

t = [1,688 ±√ (1,688² + 4 1,565)] / 2

t = [1,688 + - 2,819] / 2

t₁ = 2.25 s

t₂ = -0.57 s

Time cannot be negative so the correct result is t = 2.25 s, let's find what horizontal distance it reaches with this time

x = v₀ₓ t

x = 7.99 2.25

x = 17,978 m