Question

Find the X intercepts of the parabola with vertex (1,405) and Y intercept (0,400)

Answer 1

Explanation:

The standard form of a parabola is

`y=ax^2+bx+c`

If we know the y intercept is (0, 400), that means that when x = 0, y = 400. That allows us to begin by finding c:

`400=a(0)^2+b(0)+c` and c = 400.

Now to find a and b. Using the fact that the vertex is (1, 405), we know that h is 1 and k is 405. If

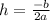`h=(-b)/(2a)` and h = 1, then

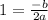`1=(-b)/(2a)` and

2a = -b so

b = -2a. Save that for a minute or two.

If

`k=c-(b^2)/(4a)` and k = 405, then

`405=400-((-2a)^2)/(4a)` and

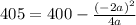`405=400-(4a^2)/(4a)` and

405 = 400 - 4a and

5 = -4a so

`a=-(5)/(4)`

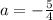
We will use that a value now to find the value of b. If b = -2a, then

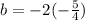`b=-2(-(5)/(4))` and

`b=(10)/(4)`

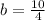
Writing our parabolic equation now:

`y=-(5)/(4)x^2+(10)/(4)x+400`

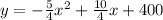
Finding the x-intercepts is just another way of saying "factor this quadratic" so we will begin that by setting the quadratic equal to 0:

`0=-(5)/(4)x^2+(10)/(4)x+400` and who hates all those fractions more than I do? Probably nobody, so we are going to get rid of them by multiplying everything by 4 to get

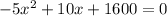`-5x^2+10x+1600=0` Assuming you can throw that into the quadratic formula to solve for the 2 values of x where y = 0, you'll find that the x-intercepts are

x = -16.91647287 and 18.91647287

Answer 2

Answer: ( -8,0),(10,0)

Explanation: