Question

Which of the following is equivalent to Root of 54?

Answer 1

• 
  `\boxed{\sf{3√(6)}}`

Explanation:

You need to find the equivalent of 54 by solving and finding the root of it.

GIVEN:

2*3³

3³=27

2*27=54

Change to square root.

`\sf{√(2*3^3)}`

Use the exponent rule.

EXPONENT RULE:

`\Longrightarrow: \sf{\:A^(B+C)=A^B\cdot \:A^C}}`

`\Longrightarrow: \sf{√(2\cdot \:3^2\cdot \:3)}`

`\sf{√(2\cdot \:3^2\cdot \:3)=√(3^2)√(2\cdot \:3)}`

`\Longrightarrow: \sf{√(3^2)=3}`

`\sf{3√(2*\:3)}`

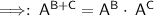
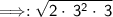
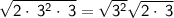
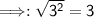
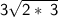
Then, you multiply the numbers from left to right.

2*3=6

SOLUTIONS:

`\Longrightarrow: \boxed{\sf{3√(6)}}`

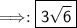
• Therefore, the equivalent to square root of 54 is "3√6", which is the correct answer.

I hope this helps. Let me know if you have any questions.