Question

Weinstein, McDermott, and Roediger (2010) report that students who were given questions to be answered while studying new material had better scores when tested on the material compared to students who were simply given an opportunity to reread the material. In a similar study, an instructor in a large psychology class gave one group of students questions to be answered while studying for the final exam. The overall average for the exam was μ = 73.4, but the n = 16 students who answered questions had a mean of M = 78.3 with a standard deviation of s = 8.4. For this study, did answering questions while studying produce significantly higher exam scores? Use a one-tailed test with α = .01 and the Distributions tool to help. (Round your answers to three decimal places, when needed.)

Answer 1

We conclude that answering questions while studying produces smaller or equal exam scores.

Explanation:

We are given that an instructor in a large psychology class gave one group of students questions to be answered while studying for the final exam.

The overall average for the exam was μ = 73.4, but the n = 16 students who answered questions had a mean of M = 78.3 with a standard deviation of s = 8.4.

Let
`\mu` = overall average for the exam.

So, Null Hypothesis,
`H_0` :
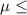`\mu \leq` 73.4 {means that answering questions while studying produce smaller or equal exam scores}

Alternate Hypothesis,
`H_A` :
`\mu` > 73.4 {means that answering questions while studying produce significantly higher exam scores}

The test statistics that would be used here One-sample t-test statistics as we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean score = 78.3

s = sample standard deviation = 8.4

n = sample of students = 16

So, the test statistics =
`(78.3-73.4)/((8.4)/(√(16) ) )` ~
`t_1_5`

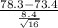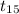
= 2.33

The value of t-test statistic is 2.333.

Now at the 0.01 significance level, the t table gives a critical value of 2.602 at 15 degrees of freedom for the right-tailed test.

Since our test statistic is less than the critical value of t as 2.333 < 2.602, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that answering questions while studying produces smaller or equal exam scores.