Answer:
The graph will show an initial value that is lower on the y-axis
Explanation:
The exponential function has the next general form:
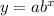
where a is the initial amount and b is the base.
If the a value in the function is decreased, but remains greater than 0, the y-intercept of the curve decrease.