Answer:
It's position at time t = 5 is 593.
Explanation:
The velocity v(t) is the integral of the acceleration a(t)
The position s(t) is the integral of the velocity v(t)
We have that:
The acceleration is:
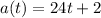
Velocity:
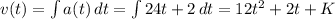
K is the initial velocity, that is v(0). Since V(0) = 13, K = 13
Then
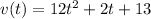
Position:
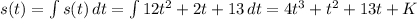
Since s(0) = 3

What is its position at time t=5?
This is s(5).


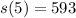
It's position at time t = 5 is 593.