Question

Too much cholesterol in the blood can increase the risk of heart disease. Young women are generally less afflicted with high cholesterol than other groups. The cholesterol levels for women aged 20-34 follow an approximately normal distribution with mean 185 milligrams per deciliter (mg/dL) and standard deviation 39 mg/dL. Middle-aged men are more susceptible to high cholesterol. The cholesterol levels of men aged 55-64 are approximately normal with mean 222 mg/dL and standard deviation 37 mg/dL. Cholesterol levels above 240 mg/dL demand medical attention.

a. What percentage of women aged 20-34 have levels above 240 mg/dL?
b. What percentage of men 55-64 have levels above 240 mg/dL? Cholesterol levels from 200 -240 are considered borderline high.
c. What percentage of women aged 20-34 have levels between 200 and 240 mg/dL?
d. What percentage of men 55-64 have levels between 200 and 240 mg/dL?

Answer 1

a. 7.92% are above 240 mg/dL

b. 31.33% are above to 240 mg/dL

c. 27.1% have borderline high levels between 200 and 240 mg/dL

d. 41.06% have borderline high levels between 200 and 240 mg/dL

Explanation:

From the given information:

a. What percentage of women aged 20-34 have levels above 240 mg/dL?

`Mean ( \mu ) =185 \\ \\ Standard Deviation ( sd )=39 \\ \\ Normal Distribution = Z= X- u / sd ~ N(0,1) \\ \\ P(X > 240) = (240-185)/39 \\ \\ =(55)/(39) \\ \\ = 1.4103 \\ \\ = P ( Z >1.41) \\ \\ From \ \ Standard \ \ Normal \ \ Table \\ \\ = 0.0792 \\ \\`

= 7.92% are above 240 mg/dL

b. What percentage of men 55-64 have levels above 240 mg/dL? Cholesterol levels from 200 -240 are considered borderline high.

`Mean ( \mu ) =222 \\ \\ Standard Deviation ( sd )=37 \\ \\ Normal Distribution = Z= (X-\mu)/(sd) ~ N(0,1) \\ \\ P(X > 240) = (240-222)/(37) \\ \\ =(18)/(37) = 0.4865 \\ \\ = P ( Z >0.486) \ From \ Standard \ Normal \ Table \\ \\ = 0.3133`

=31.33% are above to 240 mg/dL

Cholesterol levels from 200 -240 are considered borderline high.

c. What percentage of women aged 20-34 have levels between 200 and 240 mg/dL?

`To \ determine \ P(a < = Z < = b) = F(b) - F(a) \\ \\ P(X < 200) = (200-185)/39`

`= 15/39 \\ \\ = 0.3846\\ \\ = P ( Z <0.3846) From \ Standard \ Normal \ Table\\ \\= 0.64974`

`P(X < 240) = (240-185)/39 \\ \\ = 55/39 = 1.4103 \\ \\ = P ( Z <1.4103) From \ Standard \ Normal \ Table \\ \\ = 0.92077 \\ \\ P(200 < X < 240) = 0.92077-0.64974 \\ \\ = 0.271 \\ \\`

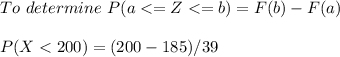
= 27.1% have borderline high levels between 200 and 240 mg/dL

d. What percentage of men 55-64 have levels between 200 and 240 mg/dL?

`To \ determine \ P(a < = Z < = b) = F(b) - F(a) \\ \\ P(X < 200) = (200-222)/37 \\ \\= -22/37 \\ \\ = -0.5946`

`= P ( Z <-0.5946) From \ Standard \ Normal \ Table \\ \\ = 0.27606`

`P(X < 240) = (240-222)/37 \\ \\ = 18/37 \\ \\ = 0.4865`

`= P ( Z <0.4865) From \ Standard \ Normal \ Table \\ \\ = 0.68669 \\ \\ P(200 < X < 240) = 0.68669-0.27606 \\ \\ = 0.4106`

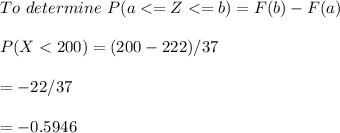
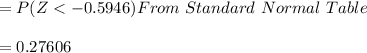
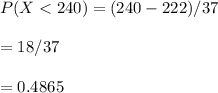
= 41.06% have borderline high levels between 200 and 240 mg/dL