Question

Use a graphing calculator to sketch the graph of the quadratic equation, and then state the domain and range y=2x^2-x+3

Answer 1

For the domain since we have a quadratic function then the domain would be all the real numbers:

`D =[x | x \in R]`

And if we want to find the range we can find the vertex:

`v_x = -(b)/(2a)= -(-1)/(2*2)= (1)/(4)`

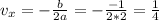
And now we can find th coordinate of y of the vertex like this:

`f(V_x) = 2((1)/(4))^2 -(1/4) +3 =2.875`

And then the range would be:

`R=[x \geq 2.875]`

Explanation:

We have the following function given:

`y = 2x^2 -x +3`

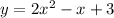
For this case we can plot the function with a calculator and we got the plot in the figure attached.

For the domain since we have a quadratic function then the domain would be all the real numbers:

`D =[x | x \in R]`

And if we want to find the range we can find the vertex:

`v_x = -(b)/(2a)= -(-1)/(2*2)= (1)/(4)`

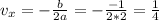
And now we can find th coordinate of y of the vertex like this:

`f(V_x) = 2((1)/(4))^2 -(1/4) +3 =2.875`

And then the range would be:

`R=[x \geq 2.875]`