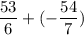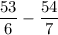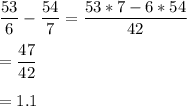Answer:
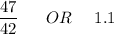
Explanation:
The objective of this question is to find the sum of the greatest and least numbers below:
![\[8\frac15, \qquad -8\frac25, \qquad -(26)/(3), \qquad -\frac{54}7, \qquad (53)/(6).\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/w6iuz0a32w1chctk2pz4500u8eb8hyl8vy.png)
To do this ; we will need to find the decimal component of each of them and equate them on a number line before summing the greatest and least numbers.
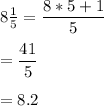
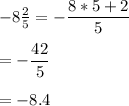
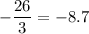
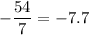
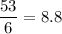
Thus; the above decimal component of the fractions given are :
8.2, -8.4, -8.7 , -7.7 and 8.8
We are to find the sum of the greatest and the smallest number ; on a number line; we will realize that the positive side is greater than the negative side , As such the greatest number from the positive side will be 8.8 and the smallest number will be -7.7
The sum of 8.8 + ( -7.7 ) = 8.8 - 7.7
= 1.1
i.e