Answer:
Explanation:
First of all, you have a typo. But that's ok, we can work around it. The equation NOT yet in standard form for an ellipse should be:
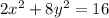
Putting it into standard form requires that the right side of the equation equals 1. That means that we need to divide everything by 16 to accomplish that. When we do that, we will get the standard form:

The general form is either
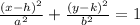 or
or
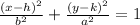
where a is ALWAYS bigger than b. So if the bigger denominator is under the x numerator, this is an ellipse that is elongated horizontally. If the larger denominator is under the y numerator, then this is an ellipse that is elongated vertically. As you can see from our standard ellipse equation, the 8 is under the x numerator, so this is a horizontally elongated ellipse.
If
 then
then
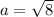 which is approximately 2.83 units.
which is approximately 2.83 units.
If
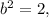 then
then
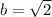 which is approximately 1.41 units.
which is approximately 1.41 units.
Since the ellipse is elongated horizontally, the a value starts at the center of the ellipse and goes 2.83 units to the right and left of the center; the b value starts at the center of the ellipse and goes 1.41 units both up and down from the center. But what's the center?
In the standard form above involving the h and the k in the numerators, the h and k indicate the coordinates of the center. h is like the x coordinate and k is like the y coordinate. Since our ellipse does not have
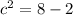 a constant in a set of parenthesis for either the x or the y term, the center is at (0, 0). From the center then, we go go both right and left to (2.83, 0) and (-2.83, 0) for the vertices of the ellipse. The co-vertices would be (0, 1.41) and (0, -1.41).
a constant in a set of parenthesis for either the x or the y term, the center is at (0, 0). From the center then, we go go both right and left to (2.83, 0) and (-2.83, 0) for the vertices of the ellipse. The co-vertices would be (0, 1.41) and (0, -1.41).
The foci have the formula (h + c, k) for the focal point to the right of the center and (h - c, k) for the focal point to the left of the center. But how do we find c?
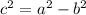
We already know that
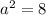 and
and
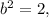 so
so
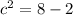 and
and
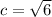
That means that the foci have the coordinates
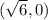 and
and
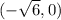
and you're done!!