Question

The equation r(t) = sin(4t)i + cos(4t)j​, 0t≥0 describes the motion of a particle moving along the unit circle. Answer the following questions about the behavior of the particle.

a. Does the particle have constant​ speed? If​ so, what is its constant​ speed?
b. Is the​ particle's acceleration vector always orthogonal to its velocity​ vector?
c. Does the particle move clockwise or counterclockwise around the​ circle?
d. Does the particle begin at the point (1,0)​?

Answer 1

a) Particle has a constant speed of 4, b) Velocity and acceleration vector are orthogonal to each other, c) Clockwise, d) False, the particle begin at the point (0,1).

Explanation:

a) Let is find first the velocity vector by differentiation:

`\vec v = (dr_(x))/(dt) i + \frac {dr_(y)}{dt} j`

`\vec v = 4\cdot \cos 4t\, i - 4 \cdot \sin 4t \,j`

`\vec v = 4 \cdot (\cos 4t \, i - \sin 4t\,j)`

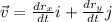
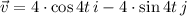
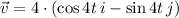
Where the resultant vector is the product of a unit vector and magnitude of the velocity vector (speed). Velocity vector has a constant speed only if magnitude of unit vector is constant in time. That is:

`\|\vec u \| = 1`

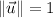
Then,

`\| \vec u \| = \sqrt{\cos^(2) 4t + \sin^(2)4t }`

`\| \vec u \| = √(1)`

`\|\vec u \| = 1`

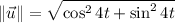
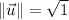
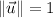
Hence, the particle has a constant speed of 4.

b) The acceleration vector is obtained by deriving the velocity vector.

`\vec a = (dv_(x))/(dt) i + \frac {dv_(y)}{dt} j`

`\vec a = 16\cdot (-\sin 4t \,i -\cos 4t \,j)`

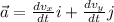
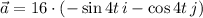
Velocity and acceleration are orthogonal to each other only if
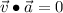`\vec v \bullet \vec a = 0`. Then,

`\vec v \bullet \vec a = 64 \cdot (\cos 4t)\cdot (-\sin 4t) + 64 \cdot (-\sin 4t) \cdot (-\cos 4t)`

`\vec v \bullet \vec a = -64\cdot \sin 4t\cdot \cos 4t + 64 \cdot \sin 4t \cdot \cos 4t`

`\vec v \bullet \vec a = 0`

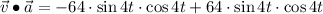
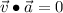
Which demonstrates the orthogonality between velocity and acceleration vectors.

c) The particle is rotating clockwise as right-hand rule is applied to model vectors in 2 and 3 dimensions, which are associated with positive angles for position vector. That is:
`t \geq 0`

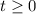
And cosine decrease and sine increase inasmuch as t becomes bigger.

d) Let evaluate the vector in
`t = 0`.

`r(0) = \sin (4\cdot 0) \,i + \cos (4\cdot 0)\,j`

`r(0) = 0\,i + 1 \,j`

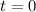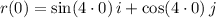
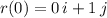
False, the particle begin at the point (0,1).