Question

In the diagram, the length of segment BC is 23 units. Line l is a perpendicular bisector of line segment A C. It intersects line segment A C at point B. Line l also contains point D. Line segment A B is 2 x + 7. Line segment A D is 4 x + 1. What is the length of segment DC? 13 units 18 units 33 units 46 units

Answer 1

C. 33

Explanation:

EDG 2020

Answer 2

The length of segment DC is 33 units.

Explanation:

A perpendicular bisector of line segment divides the line into two equal parts at 90°.

This implies that the perpendicular bisector of line segment AC at B divides the line Ac into two equal parts AB and BC.

It is given that:

BC = 23 units

AB = 2x + 7 units

AD = 4x + 1 units

The measure of AB is 23 units, according to the perpendicular bisector definition.

Compute the value of x as follows:

AB = 2x + 7

23 = 2x + 7

2x = 23 - 7

2x = 16

x = 8 units

Then the measure of side AD is:

AD = 4x + 1

= 4 × 8 + 1

= 32 + 1

= 33 units

Consider the diagram below.

Consider the right-angled triangle ABD.

Use Pythagoras theorem to compute the length of DB² as follows:

`AD^(2)=DB^(2)+AB^(2)\\\\33^(2)=DB^(2)+23^(2)\\\\DB^(2)=560`

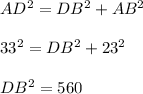
Consider the right angles triangle DBC.

Use Pythagoras theorem to compute the length of DC² as follows:

`DC^(2)=DB^(2)+BC^(2)\\\\=560+23^(2)\\\\=560+529\\\\=1089\\\\DC=√(1089)\\\\=33`

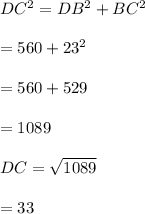
Thus, the length of segment DC is 33 units.