Question

Determine whether [1 0 3 , −3 1 −7 , 5 −1 13] is a basis for set of real numbers R cubed 3. If the set is not a​ basis, determine whether the set is linearly independent and whether the set spans set of real numbers R cubed 3.

Answer 1

The set is not a basis. It is not linearly independent and doesn't span the given vector space

Explanation:

Let u = (1,0,3), v = (-3,1,-7) and w=(5,-1,13). We want to check if the set {u,v,w} is a basis for
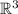`\mathbb{R}^3`. By definition, a basis is a linearly independent set that spans the vector space. So, if it is a basis, it automatically is linearly independent and spans the whole space. Since we have 3 vectors in

`A=\left[\begin{matrix}1 & -3 & 5 \\ 0 & 1 & -1 \\ 3 & -7 & 13 \end{matrix}\right]`

which is the matrix whose columns are u,v,w. To check that the set {u,v,w} is linearly independent,it is equivalent to check that the row-echelon form of A has 3 pivots.

The step by step calculation of the row-echelon form of A is ommited. However, the row-echelon form of A is

`A=\left[\begin{matrix}1 & 0 & 2 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{matrix}\right]`

In this case, we have only 2 pivots on the first and second column. This means that the columns 1,2 of matrix A are linearly independent. Hence, the set {u,v,w} is not linearly independent, and thus, it can't be a basis for
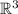`\mathbb{R}^3`. Since it is not a basis, it can't span the space.