Answer:
a. 4.77 W/

b. 2.122 W/

c. 13.78 W/

d. 69 km
Step-by-step explanation:
a.
power P of speaker = 60 W
distance d of speaker = 1.0 m
intensity I of speaker = P/4π
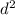
I = 60/(4 x 3.142 x
 ) = 60/12.568
) = 60/12.568
Intensity = 4.77 W/

b.
at a distance of 1.5 m, intensity will be
I = P/4π
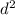
I = 60/(4 x 3.142 x
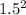 ) = 60/28.278
) = 60/28.278
Intensity = 2.122 W/

c.
combined intensity of the two front speakers will be 2 x 4.77 = 9.54 W/

combined intensity of the two back speaker will be 2 x 2.122 = 4.244 W/

total sound intensity perceived by the driver will be the superimposition of these four speakers.
I = 9.54 + 4.244 = 13.78 W/

d.
Minimum discernible intensity of sound =
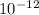 W/
W/

each speaker produces 0.06 W of power.
We assume that each speaker spreads outward evenly.
from I = P/4π
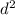 ,
,
d =
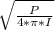
d =
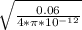 = 69094.35 m ≅ 69 km
= 69094.35 m ≅ 69 km