Question

A perpendicular bisector, , is drawn through point C on .

If the coordinates of point A are (-3, 2) and the coordinates of point B are (7, 6), the x-intercept of is . Point lies on .

Answer 1

Hi!!!!!!!!!!

If the coordinates of point A are (-3, 2) and the coordinates of point B are (7, 6), the x-intercept of CD is (18/5, 0). Point (32, -71) lies on CD.

Explanation:

Just did this on edmentum :P

Answer 2

The x-intercept of CD is B(18/5,0). The point C(32,-71) lies on the line CD.

Explanation:

the x-intercept of CD is[ A(3,0) B(18/5,0) C(9,0) D(45/2,0) ] . Point [ A(-52,117) B(-20,57) C(32,-71) D(-54,-128) ] lies on CD.

Given :

CD is perpendicular bisector of AB.

The coordinates of point A are (-3, 2) and the coordinates of point B are (7, 6).

C is the midpoint of AB.

`C=((x_1+x_2)/(2),(y_1+y_2)/(2))=((7-3)/(2),(2+6)/(2))=(2,4)`

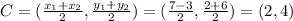
The coordinates of C are (2,4).

Line AB has a slope of:
`m_1=(y_2-y_1)/(x_2-x_1)=(6-2)/(7-(-3))=(4)/(10)=(2)/(5)`

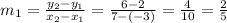
The product of slopes of two perpendicular lines is -1. Since the line CD is perpendicular to AB, therefore the slope of CD :
`m_2=-(5)/(2)`

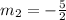
The point slope form of a line is given by:

`y-y_1=m(x-x_1)`

The slope of line CD is
`-(5)/(2)` and the line passing through the point (2,4), the equation of line CD can be written as:

`y-4=-(5)/(2)(x-2)\\y=-(5)/(2)x+5+4\\y=-(5)/(2)x+9 .... (1)`

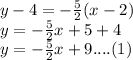
The equation of CD is
`y=-(5)/(2)x+9`

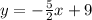
In order to find the x-intercept, put y=0.

`0=-(5)/(2)x+9\\(5)/(2)x=9\\x=(18)/(5)`

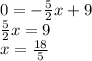
Therefore the x-intercept of CD is B(18/5,0).

Put x=-52 in eq(1).

`y=-(5)/(2)(-52)+9=139`

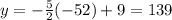
Put x=-20 in eq(1).

`y=-(5)/(2)(-20)+9=59`

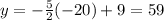
Put x=32 in eq(1)

`y=-(5)/(2)(32)+9=-71`

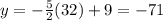
Put x=-54 in eq1).

`y=-(5)/(2)(-54)+9=144`

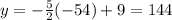
Thus, only point (32,-71) satisfies the equation of CD. Therefore the point C(32,-71) lies on the line CD.