Answer:
Explanation:
Hello!
Given the variables
X: number of days it takes to recover a drift bottle after release.
Y: distance from point of release to point of recovery (km/100)
X: 75; 76; 35; 91; 203
Y: 14.7; 19.6; 5.4; 11.7; 35.2
a)
n=5
∑X= 75 + 76 + 35 + 91 + 203= 480
∑X²= 75² + 76² + 35² + 91² + 203²= 62116
∑Y= 14.7 + 19.6 + 5.4 + 11.7 + 35.2=86.60
∑Y²= 14.7² + 19.6² + 5.4² + 11.7² + 35.2²= 2005.34
∑XY= (75*14.7) + (76*19.6) + (35*5.4) + (91*11.7) + (203*35.2)= 10991.40
![r= \frac{sumXY-((sumX)(sumY))/(n) }{\sqrt{[sumX^2-((sumX)^2)/(n) ][sumY^2-((sumY)^2)/(n) ]} } = \frac{10991.40-(480*86.60)/(5) }{\sqrt{[62116-(480^2)/(5) ][2005.34-(86.60^2)/(5) ]} } = 0.94](https://img.qammunity.org/2021/formulas/mathematics/college/6rsi7hqx81935xtxtwf8g7hbqrgq8sqby4.png)
b)
The claim is that there is a positive association between these two variables, symbolically ρ > 0
H₀: ρ ≤ 0
H₁: ρ > 0
α: 0.01
The statistic is
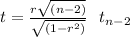
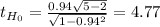
This test is one-tailed to the right, meaning that you'll reject the null hypothesis to high values of t. There is only one critical value that defined the rejection region and it is:
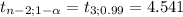
The rejection region is t ≥ 4.541
The calculated value is greater than the critical value, so the decision is to reject the null hypothesis.
Conclusion
A) Reject the null hypothesis, there is sufficient evidence that ρ > 0.
c)
The estimated regression equation is
^Y= a + bX
a= Y[bar] -bX[bar]
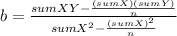
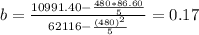
Y[bar]= ∑Y/n= 86.60/5= 17.32
X[bar]= ∑X/n= 480/5= 96
a= 17.32 - 0.17*96= 1.29
The estimated regression line is ^Y= 1.29 + 0.17X
And the estimated variance Se²
![S_e^2= (1)/(n-2)[(sumY^2-((sumY)^2)/(n) )-b^2(sumX^2-((sumX)^2)/(n) )]](https://img.qammunity.org/2021/formulas/mathematics/college/3bdyrvivbp5ic6qmkvx9odjgfenixepk8x.png)
![S_e^2= (1)/(3)[(2005.34-((86.60)^2)/(5) )-(0.17)^2(62116-((480)^2)/(5) )] = 19.42](https://img.qammunity.org/2021/formulas/mathematics/college/cy82bs7sdxzyv7ophqkughdv5sixvfecdi.png)
Se= 4.406= 4.41
d)
You have to find the value of ^Y/X=60 days, simply replace the value of X on the estimated equation:
^Y= 1.29 + 0.17*60= 11.49
The distance the bottle will travel if it drifts for 60 days will be 11.49 km/100
e)
90% CI for ^Y/X₀= 60
(a+bX₀) ±
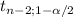 *
*
![\sqrt{S_e^2((1)/(n) + ((x_0-X[bar])^2)/(sumX^2-((sumX)^2)/(n) ) )}](https://img.qammunity.org/2021/formulas/mathematics/college/2zqo380stu48j1d673fydy8prmys3snxhd.png)
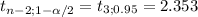
11.49 ± 2.353 *
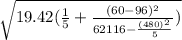
[5.99; 16.98]km/100
f)
The hypotheses are:
H₀: β ≤ 0
H₁: β > 0
α: 0.01
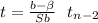
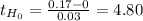
This hypothesis test is one-tailed to the right, the critical value is:
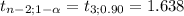
The rejection region is t ≥ 1.638, since the calculated statistic is greater than the critical value, the decision is to reject the null hypothesis. Then there is a positive linear regression between the distance from the release point and the number of days a bottle drifted.
Conclusion:
A) Reject the null hypothesis, there is sufficient evidence that β > 0.
I hope this helps!