Answer:
25.0 grams is the mass of the steel bar.
Step-by-step explanation:
Heat gained by steel bar will be equal to heat lost by the water
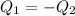
Mass of steel=
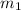
Specific heat capacity of steel =
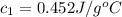
Initial temperature of the steel =
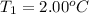
Final temperature of the steel =
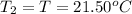
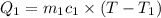
Mass of water=
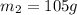
Specific heat capacity of water=
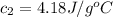
Initial temperature of the water =
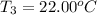
Final temperature of water =
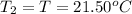
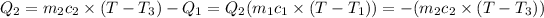
On substituting all values:
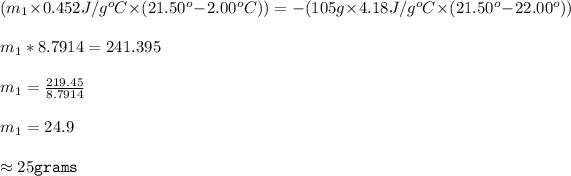
25.0 grams is the mass of the steel bar.