Question

Which formula can be used to describe the sequence? Negative two-thirds, −4, −24, −144,... f(x) = 6(negative two-thirds) Superscript x minus 1 f(x) = −6(Two-thirds) Superscript x minus 1 f(x) = Negative two-thirds(6)x − 1 f(x) = Two-thirds(−6)x − 1

Answer 1

Answer: C. f(x) = Negative two-thirds(6)x − 1

Step-by-step explanation: On Edge!!!!!

Answer 2

ƒ(x) = -⅔(6)ˣ⁻¹

Explanation:

Your geometric series is

-⅔, -4, -24, -144 …

The formula for the nth term of a geometric series is

aₙ = a₁rⁿ⁻¹

1. Calculate the common ratio (r)

`(a_(2))/( a_(1))= (-4)/(-2/3)} = 4 * (3)/(2) = 6\\\\(a_(3))/( a_(2))= (-24)/(-4) = 6\\\\(a_(4))/( a_(3))= (-144)/(-24) = 6`

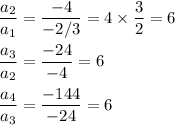
The common ratio is 6.

2. Write the formula for the series

The formula for the nth term is

aₙ = -⅔(6)ⁿ⁻¹ or

ƒ(x) = -⅔(6)ˣ⁻¹

Check:

a₁ = -⅔(6)⁰ = -⅔ × 1 = - ⅔

a₂ = -⅔(6)¹ = -⅔ × 6 = - 4

a₃ = -⅔(6)² = -⅔ × 36 = - 24

a₄ = -⅔(6)³ = -⅔ × 216 = -144

It checks.