Question

For this exercise assume that all matrices are ntimesn. Each part of this exercise is an implication of the form​ "If "statement​ 1", then​ "statement 2"." Mark an implication as True if the truth of​ "statement 2" always follows whenever​ "statement 1" happens to be true. An implication is False if there is an instance in which​ "statement 2" is false but​ "statement 1" is true. Complete parts​ (a) through​ (e). Justify each answer.

a. If there is an ntimesn matrix D such that AD equals​I, then there is also an ntimesn matrix C such that CA equalsI. Choose the correct answer below.
A. False; by the Invertible Matrix Theorem if the equation Ax 0 has only the trivial solution, then the matrix is not invertible Thus, A cannot be row equivalent to the nxn identity matrix
B. True: by the Invertible Matrix Theorem if equation Ax= 0 has only the trivial solution, then the equation matrix is not invertible. Thus, A cannot be row equivalent to the nxn identity matrix. Ax - b has no solutions for each b in R". Thus, A must also be row equivalent to the n x n identity matrix °
C. True; by the Invertible Matrix Theorem if the equation Ax=0 has only the trivial solution, then the matrix is invertible. Thus, A must also be row equivalent to the n x n identity matrix.
D. False; by the Invertible Matrix Theorem if the equation Ax 0 has only the trivial solution, then the matrix is not invertible; this means the columns of A do not span R". Thus, A must also be row equivalent to the nx n identity matrix

Answer 1

C. True; by the Invertible Matrix Theorem if the equation Ax=0 has only the trivial solution, then the matrix is invertible. Thus, A must also be row equivalent to the n x n identity matrix.

Explanation:

The Invertible matrix Theorem is a Theorem which gives a list of equivalent conditions for an n X n matrix to have an inverse. For the sake of this question, we would look at only the conditions needed to answer the question.

• There is an n×n matrix C such that CA=
  `I_n`.
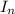• There is an n×n matrix D such that AD=
  `I_n`.
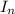• The equation Ax=0 has only the trivial solution x=0.
• A is row-equivalent to the n×n identity matrix
  `I_n`.
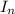• For each column vector b in
  `R^n`, the equation Ax=b has a unique solution.
• The columns of A span
  `R^n`.

Therefore the statement:

If there is an n X n matrix D such that AD=​I, then there is also an n X n matrix C such that CA = I is true by the conditions for invertibility of matrix:

• The equation Ax=0 has only the trivial solution x=0.

• A is row-equivalent to the n×n identity matrix
  `I_n`.

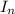The correct option is C.