Answer:
Therefore, after long period of time 80kg of salt will remain in tank
Step-by-step explanation:
given amount of salt at time t is A(t)
initial amount of salt =300 gm =0.3kg
=>A(0)=0.3
rate of salt inflow =5*0.4= 2 kg/min
rate of salt out flow =5*A/(200)=A/40
rate of change of salt at time t , dA/dt= rate of salt inflow- ratew of salt outflow
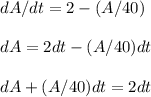
integrating factor
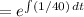
integrating factor

multiply on both sides by

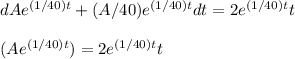
integrate on both sides

b)
after long period of time means t - > ∞
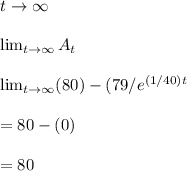
Therefore, after long period of time 80kg of salt will remain in tank