Question

A new product's sales and profits are uncertain. The marketing department has predicted that sales might be as high as 10,000 units per year with a probability of 10%. The most likely value is 7000 units annually. The pessimistic value is estimated to be 5000 units annually with a probability of 20%. Manufacturing and marketing together have estimated the most likely unit profit to be $32. The pessimistic value of $24 has a probability of 0.3, and the optimistic value of $38 has a probability of 0.2. Construct a probability distribution for the annual profit. Assume that the sales and unit profits are statistically independent. (Answers: 1. Prob. 0.2, Unit Profit $24.00, 2. Prob. 0.3; Sales $7000, 3. Prob. 0.7, Unit Profit $32.00, 4. Prob. 0.5; and Sales $10,000, 5. Prob. 0.1, Unit Profit $38.00, 6. Prob. 0.2, Sales $5000

Answer 1

Complete Question

Calculate the annual expected profit.

Answer:

`\left|\begin{array}c---&---&---&---\\$Unit Profit(X)&\$38&\$32&\$24\\P(X)&0.1&0.7&0.2\\\end{array}\right|`

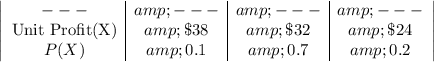
Annual Expected Profit=$213,900

Explanation:

Optimistic Probability= 10%=0.1

Pessimistic probability= 20%=0.2

Therefore, probability of the most likely unit (7000)=1-(0.2+0.1)=0.7

Given the Units, Probability of sales of each number of units and projected profit from at each level of sales

`\left|\begin{array}c---&---&---&---\\$Units&10000&7000&5000\\P(X)&0.1&0.7&0.2\\$Unit Profit&\$38&\$32&\$24\end{array}\right|`

Profit = Number of Units X Unit Profits

Therefore, a probability distribution for the annual profit is:

`\left|\begin{array}c---&---&---&---\\$Unit Profit(X)&\$38&\$32&\$24\\P(X)&0.1&0.7&0.2\\\end{array}\right|`

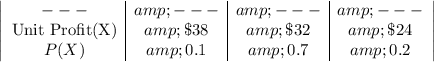
Expected Unit Profit

= (38*0.1)+(32*0.7)+(24*0.2)

=$31

Expected Sales

=(10000*0.1)+(7000*0.7)+(5000*0.2)

=6900 Units

Yearly Expected Profit =6900*$31

=$213,900