Answer:
a)
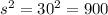
b)
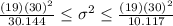
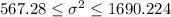
c)

Explanation:
Assuming the following question: Because of staffing decisions, managers of the Gibson-Marimont Hotel are interested in the variability in the number of rooms occupied per day during a particular season of the year. A sample of 20 days of operation shows a sample mean of 290 rooms occupied per day and a sample standard deviation of 30 rooms
Part a
For this case the best point of estimate for the population variance would be:
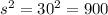
Part b
The confidence interval for the population variance is given by the following formula:

The degrees of freedom are given by:
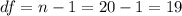
Since the Confidence is 0.90 or 90%, the significance
 and
and
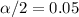 , the critical values for this case are:
, the critical values for this case are:
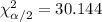

And replacing into the formula for the interval we got:
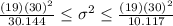
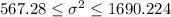
Part c
Now we just take square root on both sides of the interval and we got:
