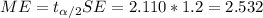Question

Overeating for just four weeks can increase fat mass and weight over two years later, a Swedish study shows.Researchers recruited 18 healthy and normal-weight people with an average age of 26. For a four-week period, participants increased calorie intake by (mostly by eating fast food) and limited daily activity to a maximum of 5000 steps per day (considered sedentary). Not surprisingly, weight and body fat of the participants went up significantly during the study and then decreased after the study ended. Participants are believed to have returned to the diet and lifestyle they had before the experiment. However, two and a half years after the experiment, the mean weight gain for participants was 6.8 lbs with a standard error of 1.2 lbs. A control group that did not binge had no change in weight.

Required:
a. Give a 95% confidence interval for parameter.
b. Give the margin of error.

Answer 1

a)
`6.8 -2.110*1.2 =4.268`

`6.8 +2.110*1.2 =9.332`

b)
`ME = t_(\alpha/2) SE= 2.110*1.2= 2.532`

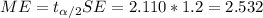
Explanation:

For this case we have the following info given:

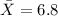`\bar X= 6.8` represent the sample mean

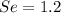`Se= 1.2` represent the standard error

`n =18` the sample size

Part a

For this case the confidence interval for the mean is given by:

`\bar X \pm t_(\alpha/2) SE`

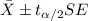
The degrees of freedom are given by:

`df =n-1=18-1=17`

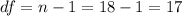
And the critical value for a confidence interval of 95% is given by:

`t_(\alpha/2)=2.110`

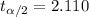
And the confidence interval would be:

`6.8 -2.110*1.2 =4.268`

`6.8 +2.110*1.2 =9.332`

Part b

The margin of error is given by:

`ME = t_(\alpha/2) SE= 2.110*1.2= 2.532`