Answer:
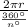 best completes this argument
best completes this argument
Explanation:
Circumference of circle =
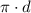
Where d is the diameter of circle
We are given that if equally sized central angles, each with a measure of n°, are drawn, the number of sectors that are formed will be equal to
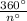
So, Number of sectors =
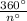
The arc length of each sector is the circumference divided by the number of sectors
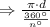
Diameter d = 2r (r = radius)
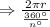
Option b is true
Hence
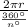 best completes this argument
best completes this argument