Answer:
The maximum torque is

Step-by-step explanation:
From the question we are told that
The length of the wire is

The current flowing through the wire is
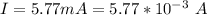
The magnetic field is

The maximum torque is mathematically evaluated as
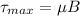
Where
 is the magnetic dipole moment which is mathematically represented as
is the magnetic dipole moment which is mathematically represented as
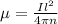
Where
 is the number of turns which from the question is 1
is the number of turns which from the question is 1
substituting values
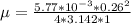
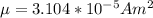
Now

