Question

A calculator is required to obtain the final answer on this question. A solid metal sphere at room temperature 20oC is dropped into a container of boiling water (100oC). If the temperature of the sphere increases 15o in 9 seconds, find the temperature of the ball after 18 seconds in the boiling water. (Assume the sphere obeys Newton's Law of Cooling.)

Answer 1

T = 47.1875°C

Explanation:

Given:

Surrounding temp, Ts = 100°C

Initial Temperature ,T0= 20°C

Increase in temperature = 15°C

Final temperature, T = 20 + 15 = 35°C

Time, t = 9 seconds

Let's take Newton's law of cooling:

`T - Ts = (T_0 - Ts)e^k^t`

We'll solve for k

`35 - 100 = (20 - 100)e^9^k`

`-65 = (-80)e^9^k`

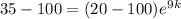
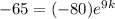
Divide both sides by -5

`13 = (16)e^9^k`

`9k = ln ((13)/(16))`

`k = (1)/(9) ln ((13)/(16))`

`k = -0.02307104053`

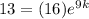
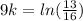
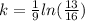
Let's now find the temperature of the ball after 18 seconds in boiling water.

Use the Newton's equation again:

`T - Ts = (T_0 - Ts)e^k^t`

`T - 100 = (20 - 100)e^-0.0^2^3^0^7^1^0^4^0^5^3^*^1^8`

`T - 100 = (-80)e^-0.0^2^3^0^7^1^0^4^0^5^3^*^1^8`

`T - 100= -52.8125`

`T = 100 - 52.8125`

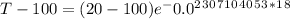
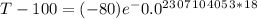
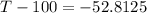
T = 47.1875°C

Temperature of the ball after 18 seconds in boiling water is 47.1875°C