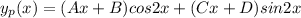Answer:
Explanation:
1 ) Given that
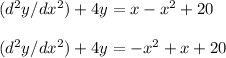
For a non homogeneous part
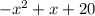 , we assume the particular solution is
, we assume the particular solution is
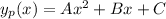
2 ) Given that
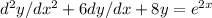
For a non homogeneous part
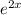 , we assume the particular solution is
, we assume the particular solution is
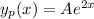
3 ) Given that
y′′ + 4y′ + 20y = −3sin(2x)
For a non homogeneous part −3sin(2x) , we assume the particular solution is
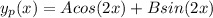
4 ) Given that
y′′ − 2y′ − 15y = 3xcos(2x)
For a non homogeneous part 3xcos(2x) , we assume the particular solution is