Question

It is found that, when exposed continuously to some fixed level of a weathering agent, a sample of 8 panels of paint coating manufactured by a certain company has a mean failure time (taken to be the time when the gloss loss reaches 50%) of xÌ… =14.10 hours with a standard deviation of s =1.67 hours.

Required:
a. Assuming the failure time is normally distributed, construct a 95% confidence interval for the true mean failure time under the same conditions.
b. Interpret the interval constructed in part (a)
c. Using the estimates of the mean and standard deviation based on the sample of 8 panels as the true mean and standard deviation of failure time of a panel (assumed to be normally distributed), find the cut-off failure time that separates, among all the panels

Answer 1

Explanation:

Hello!

The variable of interest is

X: time it takes a paint coating to reach 50% gloss loss (failure).

n= 8

X[bar]= 14.10hs

S= 1.67hs

Assuming X≈N(μ;σ²)

a) You have to estimate the average failure time using a 95% confidence interval. For this, considering that the sample size is small, and the population variance is unknown, you have to use the t-statistic:

[X[bar]±
`t_(n-1;1-\alpha /2)`*
`(S)/(√(n) )`]

`t_(n-1;1-\alpha /2)= t_(7;0.975)= 2.365`

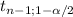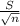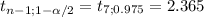
[14.10±2.365*
`(1.67)/(√(8) )`*]

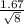[12.70; 15.49]

b) Interpretation:

Using a 95% confidence level you'd expect that the interval [12.70; 15.49]hours contains the true mean failure time for the paint coating.

c)

Using the estimates of the mean and standard deviation based on the sample of 8 panes as the true mean and standard deviation of failure time of a panel (assumed to be normally distributed), find the cut-off failure time that separates, among all the panels, the bottom 10% from the rest, i.e. the 10th percentile.

μ= 14.10

σ= 1.67

You have to find a value of the variable X that has below it 10% of the distribution, symbolically:

P(X ≤ x₀)= 0.10

To do so, you have to work using the tabulated standard normal distribution (Z) and then, using the population values μ and δ, "transform" the value of Z to a value of X. (i.e. you have to reverse the standardization to reach the corresponding value of X)

Using the Z-distribution Z= (X-μ)/σ

P(Z ≤ z₀)= 0.10

Using the left entry of the table, since we are working in the left tail of the distribution.

z₀= -1.282

Now using the formula you have to calculate the value of X

z₀= (x₀-μ)/σ

z₀*σ= x₀-μ

(z₀*σ)+μ= x₀

x₀= (z₀*σ)+μ= (-1.282*1.67) + 14.10= 11.95906 ≅ 11.96hours

The value that separates the bottom 10% of the panels from the rest is 11.96 hours.

I hope it helps!