Answer:
a)

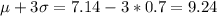
b)
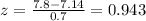
Using the normal approximation we can assume that this value 7.8 is approximately 1 deviation above the mean so then the percentage of values above is (100-68)/2 = 16%
c)
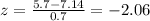
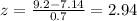
So we want to find approximately the % between 2 deviation below the mean and 3 deviation above the mean. For the % below two deviations from the mean we have (100-95)/2= 2.5% and for the % above 3 deviations from the mean we got (100-99.7)/2= 0.15% so then the percentage desired would be (100-2.5-0.15)% = 97.35%
Explanation:
Let X the random variable that represent the times for the mile run of a population, and for this case we know the distribution for X is given by:
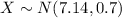
Where
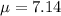 and
and

We can use the z score to find how many deviation we are from the mean with this formula:

Part a
From the empirical rule we know that we have 99.7% of the data within 3 deviations from the mean and we can calculate the range like this:

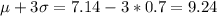
Part b
We can use the z score and we got:
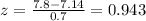
Using the normal approximation we can assume that this value 7.8 is approximately 1 deviation above the mean so then the percentage of values above is (100-68)/2 = 16%
Part c
We can use the z score formula and we got:
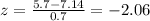
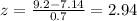
So we want to find approximately the % between 2 deviation below the mean and 3 deviation above the mean. For the % below two deviations from the mean we have (100-95)/2= 2.5% and for the % above 3 deviations from the mean we got (100-99.7)/2= 0.15% so then the percentage desired would be (100-2.5-0.15)% = 97.35%