Answer:
The solution of this system is (10,14) and it means that there are 10 three point questions and 14 five point questions.
Explanation:
In order to find the number of questions of each kind we need to solve the given system as shown below:
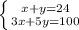
If we multiply the first equation by -3 and sum it with the second equation we can isolate the "y" variable and solve for its value:

We can use this value to find "x":
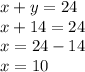
The solution of this system is (10,14) and it means that there are 10 three point questions and 14 five point questions.