Question

The function

R(x) = 80 + 7.440 √ x 0 ≤ x ≤ 15000

indicates that the monthly revenue R (in thousands of dollars) depends on the amount of dollars x spent on advertising each month.

a. By how much would the monthly revenue be expected to change if the monthly expenditure on advertising were to be raised from its current level of $ 6000 to $ 6001 ? (Use the marginal revenue R '(x) and round to the nearest dollar.) $ Incorrect
b. What is the revenue when the amount spent on advertising is $6000 . Round to the nearest dollar. $ Incorrect

Answer 1

Corrected Question

The function is:
`R(x)=80+7.440√(x) , 0\leq x\leq 15000`

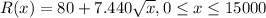
Answer:

(a)$48.02

(b)$656,299.92

Explanation:

(a) We are to determine the change in monthly revenue if the monthly expenditure, x is raised from its current level of 6000 to 6001.

`R(x)=80+7.440√(x)\\R'(x)=(d)/(dx) (80+7.440\cdot x^(1/2))\\=7.440 * (1)/(2) * x^{(1)/(2)-1}\\=3.72* x^{-(1)/(2)}\\\\R'(x)=(3.72)/(√(x) )`

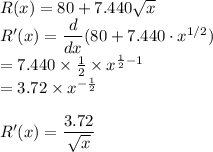
Therefore, the expected change in monthly revenue

`R'(6000)=(3.72)/(√(6000) )=$0.04802 (thousands)`

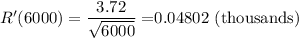
=$48.02

(b)When the amount spent on advertising is $6000

`Revenue, R(6000)=80+7.440√(6000)\\=\$656.29992$ (in thousands)\\=\$656,299.92`