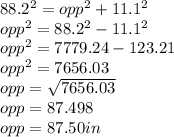Question

A stainless steel patio heater is a square pyramid. The length of one side of the base is 22.2 in. The slant height of the pyramid is 88.2 in. What is the height of the​ pyramid?

Answer 1

The height is 87.5 in

Explanation:

We can solve the height of a square pyramid using the Pythagoras theorem, this is because the slant height the height and the section of the base form a right triangle

the slant height is equivalent to the hypotenuse

the height is equivalent to the opposite

while the base(half) is the adjacent

Given

the base of the pyramid=
`22.2 in`

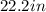
the adjacent is =
`(22.2)/(2) = 11.1 in`

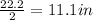
the slant height (hypotenuse)=
`88.2 in`

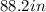
we know that Pythagoras theorem states that "The sum of the squares of the lengths of the legs of a right triangle ('a' and 'b' in the triangle) is equal to the square of the length of the hypotenuse ('c').

`c^2=a^2 + b^2`

`hyp^2=opp^2+adj^2`

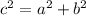
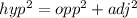
substituting we have

`88.2^2=opp^2+11.1^2\\opp^2= 88.2^2-11.1^2\\opp^2=7779.24-123.21\\opp^2=7656.03\\opp=√(7656.03) \\opp=87.498\\opp=87.50 in`