Answer:
2500
Explanation:
Monthly total cost, C(x) = 400 + 200x dollars
Monthly total revenue, R(x) =
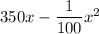 dollars
dollars
Profit = Revenue - Cost

To determine how many items, x, the firm should produce for maximum profit, we maximize P(x) by taking its derivative and solving for its critical points.

Next, we check if the point x=7500 is a maxima or a minima.
To do this, we find the second derivative of P(x).
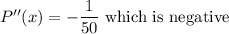
Hence, the point x=7500 is a point of maxima. However, since the firm can only produce 2500 units per month.
Therefore, the company needs to produce 2500 units to maximize profit.